
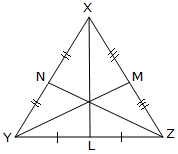


Since a triangle has 3 sides, they each have a unique altitude per side giving a total of 3 altitudes per triangles. The point of intersection is given by the solution to the systemīelow is shown the graphical solution including triangle, the altitudes of the three vertices and their point of intersection H called the orthocenter.Altitude and median are two heights used when discussing the geometry of a triangle.Īltitude of a triangle is a line segment perpendicular to a side and passing through the vertex opposing the side. The orthocenter is the point of intersection of the altitudes through O and C whose equations were found to be y = (2 / 3) x and x = 3 respectively. The equation of the altitude through A(0, 0) is given by The altitude through C, which is perpendicular to AB, is a vertical line through C(3, 3) and therefore its equation is x = 3.Ģ) The altitude through A is perpendicular to CB therefore the product of its slope m A and the slope m CB of the line through CB is equal to - 1. Therefore the line through A and B is a horizontal line. We now need to find the equation of two altitudes and their point of intersectionġ) The equation of the altitude through C is perpendicular to AB whose slope m C is given by The orthocenter is the intersection of all three altitudes from the vertices of the triangle. Y = (a y A + b y B + c y C) / (a + b + c) = (6×(0) + 5×3 + 5×(-3)) / 16 = 0īelow is shown the graphical solution including triangle, the angle bisectors of the three vertices and their point of intersection I called the incenter. Use the formula given above to find the coordinate of the incenter The x and y coordinate of the centroid are given by:īelow is shown the graphical solution including triangle, the medians of the three vertices and their point of intersection O called the centroid. ( (a x A + b x B + c x C ) / (a + b + c), (a y A + b y B + c y C ) / (a + b + c))įind the centroid of a triangle whose vertices are A(-2, 0), B(4, 3) and C(1, 6).įind the incenter of a triangle whose vertices are A(- 1, 0), B(3, 3) and C(3, - 3).įind the orthocenter of a triangle whose vertices are A(0, 0), B(5, 0) and C( 3, 3) If A(x A, y A), B(x B, y B) and C(x C, y C) are the vertices of a triangle with sides of lengths a, b and c opposite vertices A, B and C respectively, then the incenter is at: The angle bisector of a triangle is a line segment from a given vertex that divide the interior angle at the vertex into two equal angles. Which are the averages of the x and y coordinates of the vertices. X = (x A + x A + x A ) / 3, y = (y A + y B + y C ) / 3 For any triangle, all three altitudes intersect at a point called the centroid of the triangle.įor a triangle with vertices A(x A, y A), B(x B, y B) and C(x C, y C), then the centroid is at:

The median of a triangle is a line segment from a given vertex to the middle of the opposite side. For any triangle, all three altitudes intersect at a point called the orthocenter which may be inside or outside the triangle.Įxample of triangle with othocenter inside the triangle.Įxample of triangle with othocenter outside the triangle. The altitude of a triangle is a line through a given vertex of the triangle and perpendicular to the side opposite to the vertex. The altitudes, medians and angle bisectors of a Triangle are defined and problems along with their solutions are presented. Altitudes, Medians and Angle Bisectors of a Triangle


 0 kommentar(er)
0 kommentar(er)
